À chaque élection, la question des sondages, et de la confiance qu’il faut leur accorder est une des questions centrale. Nous savons qu’il peuvent se tromper, et nous avons en tête le chiffre des 3% pour un échantillon de 1000 individus, d’après un article paru dans le monde. Mais d’où vient ce chiffre, et que dire des échantillons de 500 (comme dans les sondages faits juste après le débat) ou moins (par exemple ceux portant sur les reports de voix).

On peut répondre à ces questions sans faire de calculs compliqués grâce à des simulations. En utilisant les données du dernier sondage (47.5% pour Sarkozy) et avec un échantillon de 1000 personnes, voici ce que l’on obtient:

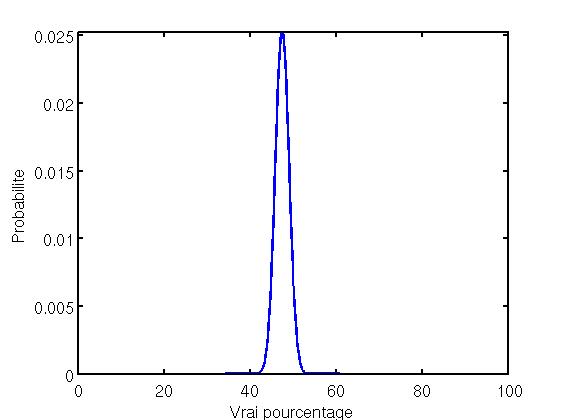
Cette courbe montre la probabilité des différents scores possibles le jour du scrutin. Le résultat le plus probable est bien entendu celui donné par le sondage, mais les résultats proches de celui-ci sont raisonnablement possibles. Cette cloche représente le degré de confiance qu’on peut accorder à ce sondage. Plus l’échantillon est important, moins cette cloche sera large.

Le chiffre qui nous intéresse est la probabilité que Nicolas Sarkozy gagne le jour de l’élection, quelque soit le score. En additionnant les probabilités de tous les scores supérieurs à 50%, on arrive à 7%. Donc, il y a 7 chances sur 100 pour que Sarkozy soit en fait le gagnant. Remarquez que ce résultat est très sensible à la taille de l’échantillon. Si on n’avait que 500 sondés, la courbe resseblerait à ça :

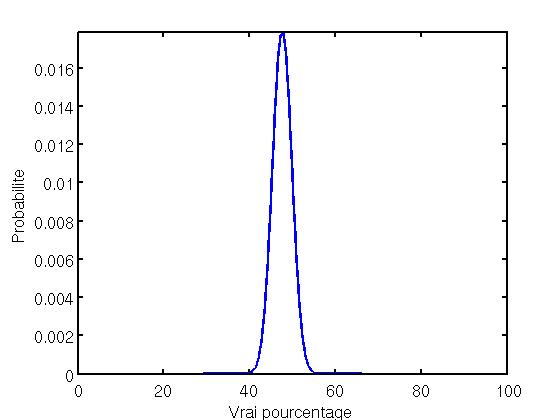
La cloche est plus large, traduisant une plus grande incertitude. La probabilité de victoire de Sarkozy serait alors de plus de 30%. Autant dire que le sondage ne sert pas à grande chose. Au passage, remarquez que même avec 1000 echantillons, c’est assez ridicule de prétendre mesurer des variations de 0,5%; à moins que les sondeurs connaissent des algorithmes relevant de la magie.

Nous (Aldo Faisal et moi) avons mis au point un petit script octave (ou Matlab) qui nous permet de visualiser la distribution de probabilité de la popularité réélle d’un candidat en fonction de sa popularité dans un échantillon donné. Il suffit de renseigner la taille de l’échantillon utilise pour le sondage (en general entre 500 et 1000) et le résultat de ce sondage (la proportion d’électeurs déclarant voter pour Sarkozy, aux alentours de 47%) et lancer le script.

clear
close all

echantillon = 500;
observation = 0.475

p=[0:0.001:1];

figure,
votesPolledSarko = round(observation*echantillon)
totalPolled = echantillon;
for ll=1:length(p)
  pSarko(ll) = binopdf(votesPolledSarko,totalPolled,p(ll));
end

plot(p*100,pSarko/sum(pSarko),'-')
probOfSarkoWin = sum(pSarko(floor(end/2):end))
axis tight
t = sprintf('Prob that Sarkzy may win is %f.'...
  probOfSarkoWin);
title(t)
xlabel('Final score')
ylabel('Probability')

Vous pouvez utiliser ce script pour générer ces courbes, ou renseigner d’autres données. Il est dans le domaine public.